光物性研究室
研究概要
並列計算
大規模並列計算技術
近年、解析的アプローチが難しい様々な問題に対して、ハミルトニアンの厳密対角化や量子モンテカルロ法などの大規模数値計算によって、多くの新たな知見が得られてきています。計算機の性能の急激な上昇に伴い、物性物理学の理論研究において大規模数値計算の果たす役割は、ますます大きくなっていくと考えられます。例えば光物性研究室では、『ランチョス法によるハミルトニアンの厳密対角化』や『時間依存シュレディンガー方程式の厳密計算』などのプログラムを作成し、低次元強相関電子系についての研究を行っており、そのさいに扱うハミルトニアン行列やベクトルの次元は数千万に達するときがあります。このような計算を行うための巨大なメモリと演算処理能力をもつ計算機として、大型ベクトルコンピュータと多くのCPUに仕事を分担させる大規模並列計算機を挙げることができます。並列計算機は、コストパーフォーマンスにおいて大型ベクトルコンピュータに対して圧倒的に優位であり、かつ、その性能は現在でも急激に向上しています。 そのため、今後ますます並列計算の重要性は増していくと思われます。しかし、大規模並列計算においては、効率の良いプログラムを作る事が極めて難しく、その性能を生かしきることができない場合が多々あります。例えば、メモリを可能な限り節約したプログラムは、図1からわかるようにCPU数を増やしても計算速度はほとんど向上しませんでした。メモリをふんだんに使ったプログラムは、並列化により計算速度が大幅に向上しますが、このプログラムの実行には極めて巨大なメモリが必要であり、メモリ量の限界のために行うことのできない計算もありました。
図はクリックすると大きなものが見られます
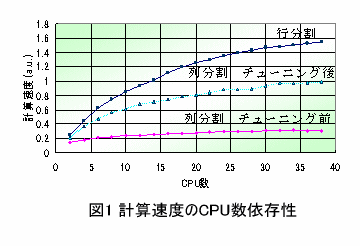
図1 計算速度のCPU数依存性
そこでメモリを節約したプログラムがなぜうまく作動しなかったかを分析し、これに基づいてこのプログラムを改良し、メモリ節約と並列化による計算速度の向上を兼ね備えるプログラムの開発しました。並列計算計算解析ツールvampirを用いて並列計算の視覚的実行時解析を行いました。計算時間の大部分を占める巨大行列と巨大ベクトルの積を計算する部分のvampir図を図2,3に示します。

図2 列分割(チューニング前)vampir図

図3 列分割(チューニング後)vampir図
これらの図においては、各CPUに対して演算を行っている時間帯は緑、オーバーヘッドと呼ばれる演算を行っていない時間帯は赤で表示されています。図2からわかるように、オーバーヘッド部分が大部分を占めており、これが並列化による速度向上がほとんどない原因でした。つまり図2の詳細な分析などから
- CPU間の仕事量のバランスが悪い
- この部分で用いられているMPIの集団通信関数は通信情報量が大きい場合には適さない
一方図3では、オーバーヘッド部分が大幅に減少していることがわかります。この場合でもオーバーヘッド部分はまだ大きいですが、通信速度の分析などから巨大な通信料に必然的にともなうオーバーヘッドであり、並列計算においては避けられないものであることが明らかになりました。
以上のようにすることで、メモリの節約と高い計算速度を兼ね備える大規模計算プログラムを開発することができました。
奈良先端科学技術大学院大学 宮本健吾 平成16年度修士論文「大規模並列計算によるランチョス法厳密対角化プログラムのチューニング」より


